Answer:
H0:
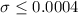
H1:
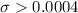
![t=(30-1) [(0.0224)/(0.02)]^2 =36.25](https://img.qammunity.org/2021/formulas/mathematics/college/7izz3hhxyjai8cqughzp5fyf43u1rfk9b7.png)
For this case since we have a right tailed test the p value is given by:
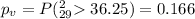
If we compare the p value and the significance level given we see that
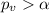 so then we have enough evidence to FAIL to reject the null hypothesis that the true population variance it's lower or equal than 0.0004 at 5% of significance.
so then we have enough evidence to FAIL to reject the null hypothesis that the true population variance it's lower or equal than 0.0004 at 5% of significance.
Explanation:
Previous concepts and notation
The chi-square test is used to check if the standard deviation of a population is equal to a specified value. We can conduct the test "two-sided test or a one-sided test".
n = 30 sample size
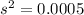 represent the sample variance
represent the sample variance
s= 0.0224 represent the sample deviation
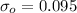 the value that we want to test
the value that we want to test
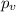 represent the p value for the test
represent the p value for the test
t represent the statistic
 significance level
significance level
State the null and alternative hypothesis
On this case we want to check if the population variance is higher than 0.0004 (the specification), so the system of hypothesis are:
H0:
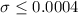
H1:
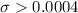
In order to check the hypothesis we need to calculate th statistic given by the following formula:
![t=(n-1) [(s)/(\sigma_o)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/zqlqe1poatrqkxg397eatbvcjabod9ldg7.png)
This statistic have a Chi Square distribution distribution with n-1 degrees of freedom.
What is the value of your test statistic?
Now we have everything to replace into the formula for the statistic and we got:
![t=(30-1) [(0.0224)/(0.02)]^2 =36.25](https://img.qammunity.org/2021/formulas/mathematics/college/7izz3hhxyjai8cqughzp5fyf43u1rfk9b7.png)
What is the critical value for the test statistic at an α = 0.05 significance level?
Since is a right tailed test the critical zone it's on the right tail of the distribution. On this case we need a quantile on the chi square distribution with df=30-1=19 degrees of freedom that accumulates 0.05 of the area on the right tail and 0.95 on the left tail.
We can calculate the critical value in excel with the following code: "=CHISQ.INV(0.95,29)". And our critical value would be
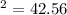
Since our calculated value is lower than the critical value we to reject the null hypothesis.
What is the approximate p-value of the test?
For this case since we have a right tailed test the p value is given by:
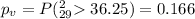
If we compare the p value and the significance level given we see that
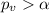 so then we have enough evidence to FAIL to reject the null hypothesis that the true population variance it's lower or equal than 0.0004 at 5% of significance.
so then we have enough evidence to FAIL to reject the null hypothesis that the true population variance it's lower or equal than 0.0004 at 5% of significance.