Answer:

Explanation:
We are given the following in the question:
The numbers of teams remaining in each round follows a geometric sequence.
Let a be the first the of the geometric sequence and r be the common ration.
The
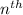 term of geometric sequence is given by:
term of geometric sequence is given by:
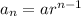

Dividing the two equations, we get,

the first term can be calculated as:

Thus, the required geometric sequence is
