Answer:
Therefore, the probability is P=0.0054.
Explanation:
You have three jars containing marbles, as follows:
jar 1: 600 red and 400 white
jar 2: 900 blue and 100 white
jar 3: 10 green and 990 white
We calculate the probability of obtaining a red a blue and a green marbles.
We conclude that each jars have 1000 marbles.
For jar 1 we have that:
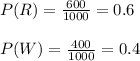
For jar 2 we have that:
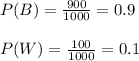
For jar 3 we have that:

Therefore, we get

Therefore, the probability is P=0.0054.