Question:
What is the common denominator of
 in the complex fraction
in the complex fraction

A)
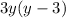
B)
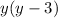
C)
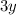
D)
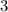
Answer:
Option D : 3 is the common denominator
Step-by-step explanation:
It is given that the complex fraction

We need to determine the common denominator of
 from the complex fraction.
from the complex fraction.
Let us consider the fraction

To find the common denominator, let us take LCM.
Thus, rewriting the above fraction as,
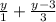
The LCM can be determined by multiplying the denominators.
Thus, we get,
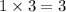
Thus, the common denominator is 3.
Hence, Option D is the correct answer.