Question

In the reaction, A → Products, a plot of 1/[A] vs. time is linear and the slope is equal to 0.056 M−1 s−1. If the initial concentration of A is 0.80 M, how long will it take one-half of the initial amount of A to react?

Answer 1

t = 22.32 s

Step-by-step explanation:

The kinetics of a reaction can be known graphically by plotting the concentration vs time experimental data on a sheet of graph.

• The concentration vs time graph of zero order reactions is linear with negative slope.
• The concentration vs time graph for a first order reactions is a exponential curve. For first order kinetics the graph between the natural logarithm of the concentration vs time comes out to be a straight graph with negative slope.
• The concentration vs time graph for a second order reaction is a hyperbolic curve. Also, for second order kinetics the graph between the reciprocal of the concentration vs time comes out to be a straight graph with positive slope.

Given that:- 1/[A] vs. time is linear which means it follows second order kinetics.

Thus,

Given that slope = k = 0.056 M⁻¹ s⁻¹.

Integrated rate law for second order kinetic is:

`(1)/([A_t]) = (1)/([A]_0)+kt`

Where,
`[A_t]` is the final concentration = Half of the initial concentration = 0.80 /2 M = 0.40 M

`[A_0]` is the initial concentration = 0.80 M

So,

`(1)/(0.40) = (1)/(0.80)+0.056* t`

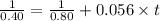
t = 22.32 s