Answer:
90% confidence interval for the population cost of a ticket = [97.85 , 103.55]
Explanation:
We are given below the airfare prices (in dollars) for a one-way ticket from Atlanta to Chicago that was chosen by Newsweek in 2001 ;
87, 90, 94, 96, 98, 99, 101, 101, 102, 103, 104, 105, 105, 107, 108, 111
We have to calculate a 90% confidence interval for the population cost of a ticket.
The Pivotal quantity is given by;
P.Q. =
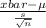 ~
~

where,
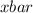 = Sample mean = Sum of all above values ÷ Total values
= Sample mean = Sum of all above values ÷ Total values
=
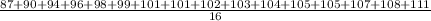 = 100.7
= 100.7
s = Sample standard deviation =
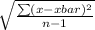 = 6.5
= 6.5
n = sample size = 16
So, 90% confidence interval for the population cost of a ticket is given by;
P(-1.753 <
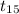 < 1.753) = 0.90
< 1.753) = 0.90
P(-1.753 <
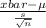 < 1.753) = 0.90
< 1.753) = 0.90
P(-1.753 *
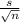 <
<
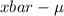 < 1.753 *
< 1.753 *
P(-xbar - 1.753 *
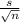 <
<
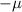 < -xbar + 1.753 *
< -xbar + 1.753 *
P(xbar - 1.753 *
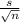 <
<
 < xbar + 1.753 *
< xbar + 1.753 *
So, 90% confidence interval for
 = [xbar - 1.753 *
= [xbar - 1.753 *
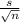 , xbar - 1.753 *
, xbar - 1.753 *
=
![[100.7 - 1.753*(6.5)/(√(16) ) , 100.7 + 1.753*(6.5)/(√(16) ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/twdsqh3oreiabi3olbr4i47msd0b0ln78a.png)
= [97.85 , 103.55]
Therefore, confidence interval for the population cost of a ticket is [97.85 , 103.55] .