Question

Two identical planets, each with a mass of 1024 kg, orbit around the midpoint between the two planets. If the distance between the two planets is 2 x 108 m (as measured from their centers), how fast is each of the planets moving in their orbit?

Answer 1

each of the planets moving = 408.35 m/s

Step-by-step explanation:

given data

mass =
`10^(24)` kg

distance between two planets = 2 ×
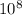`10^(8)` m

solution

if distance between two planet is 2 ×
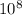`10^(8)` m it mean it's diameter so

that radius will be 1 ×
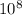`10^(8)` m

and

F =
`(G*m*m)/(2r^2)` ................1

and

F =
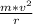`(m*v^2)/(r)` ..............2

so from equation 1 and 2 will be

`(G*m*m)/(2r^2)` =
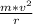
`(m*v^2)/(r)`

v =
`\sqrt{(G*m)/(4*r)}` ............2

put here value

v =
`\sqrt{(6.67*10^(-11)*10^(24))/(4*10^8)`

v = 408.35 m/s