Answer:
The quadrilateral ABCD is a rhombus.
Explanation:
A rhombus is a quadrilateral having equal sides.
If ABCD is a rhombus then,
AB = BC = CD = DA
It is provided that the coordinates of the rhombus ABCD are:
A = (-1, -5)
B = (8, 2)
C = (11, 13)
D = (2, 6)
Use the distance formula to compute the lengths of AB, BC, CD and DA.
The distance formula is:
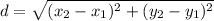
Compute the length of AB:
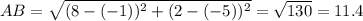
Compute the length of BC:
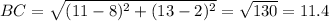
Compute the length of CD:
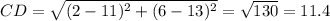
Compute the length of DA:
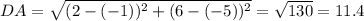
Thus, the lengths AB, BC, CD and DA are equal, i.e. all sides are of length 11.4.
Hence proved that the quadrilateral ABCD is a rhombus.