Question

The lengths of text messages are normally distributed with an unknown population mean. A random sample of text messages is taken and results in a 95% confidence interval of (23,47) characters. What is the correct interpretation of the 95% confidence interval?

Answer 1

Correct interpretation is provided below.

Explanation:

We are given that the lengths of text messages are normally distributed with an unknown population mean.

Also, a random sample of text messages is taken and results in a 95% confidence interval of (23,47) characters.

Now, the correct interpretation of the 95% confidence interval is that we are 95% confident that the population mean will lie between the 23 and 47 as the confidence interval is estimated taking into consideration the population mean only.

Answer 2

95% of the text messages have length between 23 units and 47 units.

Explanation:

We are given the following in the question:

The lengths of text messages are normally distributed.

95% confidence interval:

(23,47)

Thus, we could interpret the confidence interval as:

About 95% of the text messages have length between 23 units and 47 units.

By Empirical rule for a normally distributed data, about 95% of data lies within 2 standard deviations of mean , thus we can write:

`\mu - 2\sigma = 23\\\mu +2\sigma = 47\\\Rightarrow \mu = 35\\\Rightarrow \sigma = 6`

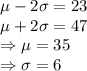
Thus, the mean length of text messages is 23 units and standard deviation is 6 units.