Question

A commuter is driving a car along a straight road at a constant speed of 21.0 m/s. Just as she passes a law officer parked along the side of the road, the officer starts to accelerate 0.50 m/s2 to overtake her. Assume that the officer maintains this?

Answer 1

The police officer takes 84 seconds to catch up to the commuter driving at a constant speed of 21.0 m/s, as calculated using the kinematic equations for uniform acceleration.

Step-by-step explanation:

The scenario provided involves kinematic equations for a commuter driving at a constant velocity and a police officer accelerating from rest. Let's determine how long it takes the police officer to catch up to the commuter.

For the commuter:

The car has a constant velocity of 21.0 m/s. Therefore, the equation for displacement is:

x = v0t

For the police officer:

The police car starts from rest and accelerates at 0.50 m/s2. The equation for displacement is:

x = 0.5 * a * t2

Setting the two displacements equal to each other, since they will be at the same point when the police car catches up, gives us:

v0t = 0.5 * a * t2

Solving for t, we get:

t = (2 * v0)/a

Substituting the given values:

t = (2 * 21.0 m/s) / (0.50 m/s2) = 84s

Therefore, it takes the police offer 84 seconds to catch up to the commuter.

Answer 2

Complete Question:

Upon searching online, the full part of the question contains these two parts:

(a) determine the time it takes the police officer to reach the commuter.

Find (b) the speed and (c) the total displacement of the officer as he overtakes the commuter.

Answer:

a) 84 seconds

b) 42 m/s

c) 1764 m

Step-by-step explanation:

a) To find the time taken for the police officer to reach the commuter, we need to set their distance traveled 's' to be equal.

Now we can solve the following two equations for the officer and commuter:

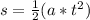`s = (1)/(2)(a*t^2)` (for the officer as his initial speed u = 0 m/s)

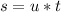`s = u*t` (for the commuter, as her initial speed is given but acceleration is 0 m/s^2)

As s is equal we can solve these equations in the following way for the time:

`(1)/(2) (0.5t^2) = 21t`

`t = 84`

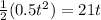
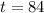
thus the time taken is 84 seconds.

b) Speed of officer = acceleration * time taken to overtake commuter

Speed of officer = 0.5 * 84 = 42 m/s

c) Total displacement = 0.5 * a * (t^2)

Total displacement = 0.5 * 0.5 * (84^2)

Total displacement = 1764 m