Question

Find the probability that when a couple has three ​children, at least one of them is a boy. ​(Assume that boys and girls are equally​ likely.)

Answer 1

The probability that at least 1 of the 3 children is a boy is 0.875.

Explanation:

The probability of a baby born being a girl or a boy is same, i.e.

P (G) = P (B) = 0.50.

A couple has 3 children.

Let X = number of boys.

The random variable X follows a Binomial distribution. The probability of a Binomial distribution is computed using the formula:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0, 1, 2...`

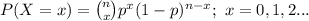
Compute the probability that at least 1 of the 3 children is a boy as follows:

P (At least 1 boy) = 1 - P (No boys)

P (X ≥ 1) = 1 - P (X = 0)

`=1-{3\choose 0}(0.50)^(0)(1-0.50)^(3-0)\\=1-(1*1*0.125)\\=1-0.125\\=0.875`

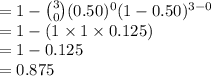
Thus, the probability that at least 1 of the 3 children is a boy is 0.875.