Question

A stone is thrown horizontally at 60.0 m/sm/s from the top of a very tall cliff. Calculate its horizontal position and vertical position at 2.00 ss intervals for the first 10.0 ss .

Answer 1

X-Positions: Y-Positions

x(0) = 0 y(0) = 0

x(2) = 120 m y(2) = 19.6 m

x(4) = 240 m y(4) = 78.4 m

x(6) = 360 m y(6) = 176.4 m

x(8) = 480 m y(8) = 313 m

x(10) = 600m y (10) = 490 m

Step-by-step explanation:

X-Positions

• First, we choose to take the horizontal direction as our x-axis, and the positive x-axis as positive.
• After being thrown, in the horizontal direction, no external influence acts on the stone, so it will continue in the same direction at the same initial speed of 60. 0 m/s
• So, in order to know the horizontal position at any time t, we can apply the definition of average velocity, rearranging terms, as follows:

`x = v_(ox) * t = 60.0 m/s * t(s)`

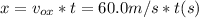
• It can be seen that after 2 s, the displacement will be 120 m, and each 2 seconds, as the speed is constant, the displacement will increase in the same 120 m each time.

Y-Positions

• We choose to take the vertical direction as our y-axis, taking the downward direction as our positive axis.
• As both axes are perpendicular each other, both movements are independent each other also, so, in the vertical direction, the stone starts from rest.
• At any moment, it is subject to the acceleration of gravity, g.
• As the acceleration is constant, we can find the vertical displacement (taking the height of the cliff as the initial reference level), using the following kinematic equation:

`y = (1)/(2) * g* t^(2) = (1)/(2) * 9.8 m/s2 * t(s)^(2)`

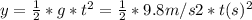
• Replacing by the values of t, we get the following vertical positions, from the height of the cliff as y = 0:
• y(2) = 2* 9.8 m/s2 = 19.6 m
• y(4) = 8* 9.8 m/s2 = 78.4 m
• y(6) = 18*9.8 m/s2 = 176.4 m
• y(8) = 32*9.8 m/s2 = 313.6 m
• y(10)= 50 * 9.8 m/s2 = 490.0 m