Question

What is the relationship between the spring constant and the period in a mass hanging on a spring oscillation and why?

Answer 1

Step-by-step explanation:

Period of a mass on a spring is:

T = 2π√(m/k)

T is inversely proportional with the square root of k. So as the spring constant increases, the period decreases.

Answer 2

`T\propto (1 )/(√(k)) \text{ and } k \propto (1)/(T^(2))`

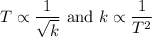
Step-by-step explanation:

The period T is inversely proportional to the square root of the spring constant, and

The spring constant is inversely proportional to the square of the period.

It all comes from Hooke's Law.

We usually get the equation for the period, but we can easily rearrange it to get an equation for the spring constant.

`\begin{array}{rcl}T &= &\mathbf{2\pi \sqrt{(m)/(k)}}\\\\T^(2) &=& 4 \pi^(2) (m)/(k)\\kT^(2)& =& 4 \pi^(2)m\\k &=& \mathbf{(4 \pi^(2)m)/(T^(2))}\end{array}`