Answer:
YTM = 7.27%
Step-by-step explanation:
We know,
Yield to Maturity (YTM) =
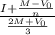
Here,
I = Coupon Payment = Coupon Rate × Par Value
M = Par Value
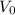 = Market value/Current value
= Market value/Current value
n = Number of years/periods.
Given,
M = $1,000
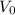 = $1,080
= $1,080
I = $1,000 × 8% = $80
n = 15 years
Putting the values into the formula, we can get...
Yield to Maturity (YTM) =
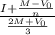
or, YTM =
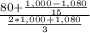
or, YTM =
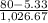
or, YTM = 0.072730
Therefore, YTM = 7.27%