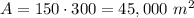Question

Farmer Ed has 600 meters of​ fencing, and wants to enclose a rectangular plot that borders on a river. If Farmer Ed does not fence the side along the​ river, find the length and width of the plot that will maximize the area. What is the largest area that can be​ enclosed?

Answer 1

The plot must have x=150 m y=300 m and its maximum area is
`45,000\ m^2`

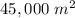
Explanation:

Maximum Values of Functions

Let f(x) be a real function and f'(x) its derivative. The values for which f'(x)=0 are called the critical points. If x=a is a critical point of f(x) and

f''(a)>0, then x=a is a minimum

f''(a)<0, then x=a is a maximum

The question requires us to maximize the area of the rectangular plot, knowing the perimeter of the fencing is 600 m.

The perimeter of a rectangle of sides x and y is

`P=2x+2y`

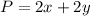
Since the side along the river (assumed to be y) won't be fenced, then the perimeter of the fence is

`P=2x+y=600`

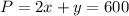
Solving for y

`y=600-2x`

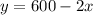
Now, the area of the rectangle is

`A=x.y`

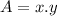
Using the relation found above:

`A=x(600-2x)=600x-2x^2`

Find the derivative

`A'=600-4x`

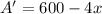
Equal to zero

`600-4x=0`

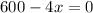
Solve for x

`x=150\ m`

Find the second derivative

`A''=-4`

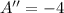
Since it's negative, the value x=150 is a maximum

The value of y is

`y=600-2\cdot 150=300\ m`

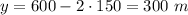
Thus, the dimensions of the plot are x=150 m, y=300 m

And the maximum area of the plot is

`A=150\cdot 300=45,000\ m^2`