Question

This figure is made up of a rectangle and parallelgram what is the area of this figure

Answer 1

40 unit²

Explanation:

If you are referring to the figure attached read on:

We know that the distance between two points can be computed using the formula:

`d = \sqrt{(X_2-X_1)^(2) + (Y_2-Y_1)^(2)}`

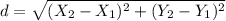
We also know that the formula for the area of a rectangle is:

A = L x W

While the area of a parallelogram is:

A = b x h

In the figure the dimensions of the parallelogram is easy to get as the base is vertical and the height is horizontal parallel to the x and y axes.

The base is 6 units, and the height is 1 unit. So we multiply that:

A = 6 x 1 = 6 units²

As for the rectangle we need to use the distance formula because they are not parallel to the x and y axes.

First let's get the width, then the length.

`L = \sqrt{(-6 - 2)^2+(-1-1)^(2) } \\\\ = √((-8)^2 + (-2)^2)\\\\ = √(64 + 4)\\\\ =√(68) \\\\ = 8.25 units\\W = √((-6 - -5)^2+(-1 - - 5)^2) \\\\ = √((-1)^2+(4)^2) \\\\ =√(1 + 16)\\\\ = √(17)\\\\ = 4.12 units\\`

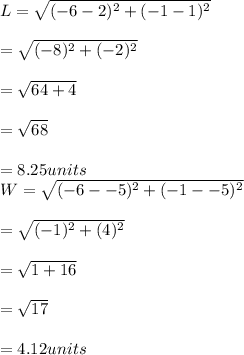
So now we have the the dimensions of the rectangle, we can solve for the area.

A = 8.25 unit x 4.12 unit

= 33.99unit²

To get the total area then, we add up their areas:

33.99 unit² + 6 unit² = 39.99 unit² ≅ 40 units²