Question

The revenue function​ R(x) and the cost function​ C(x) for a particular product are given. These functions are valid only for the specified range of values. Find the number of units that must be produced to break even.

R(x) = 200 x -x squared​; ​C(x) = 40x + 3375; ​0 less than or equal to x less than or equal to 100

The manufacturer must produce ___ units to break even.

Answer 1

The manufacturer should produce 25 units to break even

Explanation:

Revenue and Cost Function

The revenue function R(x) is given as

`R(x) = 200 x -x^2`

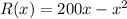
And the cost function is

`C(x) = 40x + 3375`

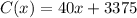
Both valid in the range

`0\leq x \leq 100`

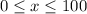
We need to find the number of units that must be produced to break even, which means that the cost and revenue are the same:

`R(x)=C(x)`

`200 x -x^2= 40x + 3375`

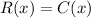
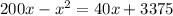
Rearranging

`x^2-160 x + 3375=0`

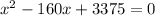
Solving for x

`x=135,\ x=25`

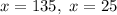
Both values are valid, but only x=25 lies in the determined range for x, thus the only solution is

x=25