Question

The number of apples sold at your store on a given day has a bell-shaped normal distribution with a median of 300 apples and a variance of 2500 squared apples. What percentage of days do you expect to sell between 250 and 400 apples? Give your answer as a percent but leave out the % sign.

Answer 1

The percentage of days that could be expected for the sale of the apples to be between 250 and 400 is 83.85.

Explanation:

The number of apples sold at the store on a given day has a bell shaped normal distribution.

The median of the distribution is given as 300 apples.

The median would represent the mean in a normal distribution,

`\mu` = 300 apples

In a normal distribution the mean is equal to the median.

The variance is given as
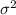`\sigma^2` = 2500

Therefore the standard deviation of the distribution can be found by taking the root of variance.

The standard deviation can be found by =
`\sigma` =
`√(\sigma^2)` =
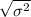`√(2500)` = 50 apples.

It is required to find the percentage of days when the store will sell between 250 and 300 apples.

Therefore we have to find the probability of the number of apples being sold is between 250 and 400 apples.

Let the number of apples being sold be X.

Therefore to find the probability by using the Z variable.

Therefore to find the probability we have to find p( 250 < X < 400).

The Z value is given by Z =
`(X - \mu)/(\sigma)`

`Z_( (X = 250)) = (250 - 300)/(50) = -1`

`Z_( (X = 400)) = (400 - 300)/(50) = 2`

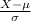
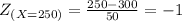
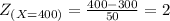
∴ p(( 250 < X < 400)

= p(-1 < Z < 2)

= p(Z<2) - p(Z<-1)

= 0.9972 - 0.1587 .... using the Z - tables we can find the probability

values

= 0.8385

To get percentage of days we simply multiply the probability by 100.

Therefore the percentage of days that could be expected for the sale of the apples to be between 250 and 400 is = 0.8385 × 100 = 83.85