Question

A two-dimensional rectangular plate is subjected to prescribed boundary conditions. Using the results of the exact solution for the heat equation presented in Section 4.2, calculate the temperatures along the mid-plane of the plate (x = 1 m) at y = 0.25, 0.5, and 0.75 m by considering the first five nonzero terms of the infinite series. Assess the error resulting from using only the first three terms of the infinite series.

Answer 1

The temperature calculated with 5 terms at (1,0.25),(1,0.5) and (1,0.75) are 71.24 C, 94.53 C and 121.14 C respectively.

The temperature calculated with 3 terms at (1,0.25),(1,0.5) and (1,0.75) are 71.24 C, 94.59 C and 121.89 C respectively.

The error percentage between two temperatures for (1,0.25),(1,0.5) and (1,0.75) is 0%, 0.06% and 0.62% respectively.

Step-by-step explanation:

From the given section, the equation of Temperature distribution is given as

`\theta(x,y) =(T-T_1)/(T_2-T_1)`

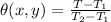
This is also given by the exact solution as

`\theta(x,y) =(2)/(\pi)\sum_(n=1)^(\theta)((-1)^(n+1)+1)/(n)sin((n\pi x)/(L))\frac{sinh({n\pi y}/{L})}{sinh({n\pi W}/{L})}`

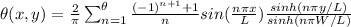
For point 1 x=1, y=0.25

From the attached diagram

L=2

W=1

x/L=1/2

y/L=1/8

W/L=1/2

So the equation becomes

`\theta(1,0.25) =(2)/(\pi)\sum_(n=1)^(\theta)((-1)^(n+1)+1)/(n)sin((n\pi )/(2))\frac{sinh({n\pi}/{8})}{sinh({n\pi}/{2})}`

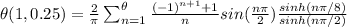
Now as seen the value of terms for n=2,4,6,8.... is zero so thus only first five odd terms (n=1,n=3,n=5,n=7,n=9) will be considered as

`\theta(1,0.25) =(2)/(\pi)[((-1)^(1+1)+1)/(1)sin((\pi )/(2))\frac{sinh({\pi}/{8})}{sinh({\pi}/{2})}+((-1)^(3+1)+1)/(3)sin((3\pi )/(2))\frac{sinh({3\pi}/{8})}{sinh({3\pi}/{2})}+`
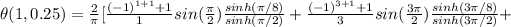
`+((-1)^(5+1)+1)/(5)sin((5\pi )/(2))\frac{sinh({5\pi}/{8})}{sinh({5\pi}/{2})}+((-1)^(7+1)+1)/(7)sin((7\pi )/(2))\frac{sinh({7\pi}/{8})}{sinh({7\pi}/{2})}+((-1)^(9+1)+1)/(9)sin((9\pi )/(2))\frac{sinh({9\pi}/{8})}{sinh({9\pi}/{2})}]`
`\theta(1,0.25) =(2)/(3.14)[0.35012+(-0.01761)+0.00108+(-0.00007)+0.00000551)\\\theta(1,0.25) =0.2124\\`

From the diagram

T_2=150

T_1=50

Now the equation becomes

`\theta(1,0.25) =(T-50)/(150-50)\\T(1,0.25) =\theta(1,0.25)({150-50})+50\\T(1,0.25) =71.24 \, C`

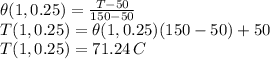
Using the 1st 3 terms the solution is given as

`\theta(1,0.25) =(2)/(3.14)[0.35012+(-0.01761)+0.00108)]\\\theta(1,0.25) =0.2124\\`

The error is 0%.

Similarly for point (1,0.5)

x/L=1/2

y/L=1/4

W/L=1/2

The solution is given as

`\theta(1,0.5) =(2)/(3.14)[0.69921]\\\theta(1,0.5) =0.4453\\`

`\theta(1,0.5) =(T-50)/(150-50)\\T(1,0.5) =\theta(1,0.5)({150-50})+50\\T(1,0.5) =94.53\, C`

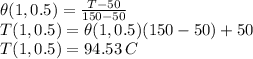
With using 1st 3 terms the value is given as

`\theta(1,0.5) =(2)/(3.14)[0.70019]\\\theta(1,0.5) =0.4459\\`

`\theta(1,0.5) =(T-50)/(150-50)\\T(1,0.5) =\theta(1,0.5)({150-50})+50\\T(1,0.5) =94.59\, C`

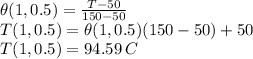
Ther error is given as

`error=(94.59-94.53)/(94.53)*100=0.06\%`

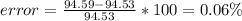
Similarly for point (1,0.75)

x/L=1/2

y/L=3/8

W/L=1/2

The solution is given as

`\theta(1,0.75) =(2)/(3.14)[1.11693]\\\theta(1,0.75) =0.7114\\`

`\theta(1,0.75) =(T-50)/(150-50)\\T(1,0.75) =\theta(1,0.75)({150-50})+50\\T(1,0.75) =121.14\, C`

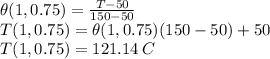
With using 1st 3 terms the value is given as

`\theta(1,0.75) =(2)/(3.14)[1.12874]\\\theta(1,0.75) =0.7189\\`

`\theta(1,0.75) =(T-50)/(150-50)\\T(1,0.75) =\theta(1,0.75)({150-50})+50\\T(1,0.75) =121.89\, C`

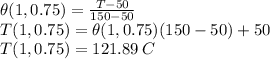
Ther error is given as

`error=(121.89-121.14)/(121.14)*100=0.62\%`

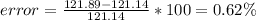
So

The temperature calculated with 5 terms at (1,0.25),(1,0.5) and (1,0.75) are 71.24 C, 94.53 C and 121.14 C respectively.

The temperature calculated with 3 terms at (1,0.25),(1,0.5) and (1,0.75) are 71.24 C, 94.59 C and 121.89 C respectively.

The error percentage between two temperatures for (1,0.25),(1,0.5) and (1,0.75) is 0%, 0.06% and 0.62% respectively.