Question

"To fill up the last week of the season, Larry's Paving bids on 6 similar but statistically independent small jobs. Larry has a 40% chance of getting each contract, and will net $200 on each contract he gets. Then he has to defray a $300 expense preparing the bids. a. What is the expected number of contracts he will get?

Answer 1

The expected number of contracts Larry will get is 2.40.

Step-by-step explanation:

Let X = number of contracts Larry will get.

The probability of Larry getting a contact is, P (X) = p = 0.40

The number of bids placed is, n = 6.

Each bid is placed on statistically independent small jobs.

The random variable X follows a Binomial distribution with parameters n = 6 and p = 0.40.

The expected value of a Binomial distribution is:

`E(X)=n* p`

Compute the expected number of contracts Larry will get as follows:

`E(X)=n* p=6*0.40=2.40`

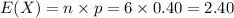
Thus, the expected number of contracts Larry will get is 2.40.