Question

Suppose that only 25% of all drivers come to a complete stop at an intersection having flashing red lights in all directions when no other cars are visible. What is the probability that, of 20 ran- domly chosen drivers coming to an intersection under these conditions, a. At most 6 will come to a complete stop

Answer 1

The probability that at most 6 will come to a complete stop is 0.7857.

Explanation:

Let X = number of drivers come to a complete stop at an intersection having flashing red lights in all directions when no other cars are visible.

The probability of the event X is, P (X) = p = 0.25.

The sample of drivers randomly selected is of size, n = 20.

The random variable X follows a binomial distribution with parameters n = 6 and p = 0.25.

The probability function of Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0,1,2,...`

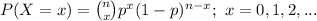
Compute the probability that at most 6 will come to a complete stop as follows:

P (X ≤ 6) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)

+ P (X = 4) + P (X = 5) + P (X = 6)

`={20\choose 0}(0.25)^(0)(1-0.25)^(20-0)+{20\choose 1}(0.25)^(1)(1-0.25)^(20-1)+{20\choose 2}(0.25)^(2)(1-0.25)^(20-2)\\...+{20\choose 0}(0.25)^(6)(1-0.25)^(20-6)\\=0.0032+0.0211+0.0669+0.1339+0.1897+0.2023+0.1686\\=0.7857`

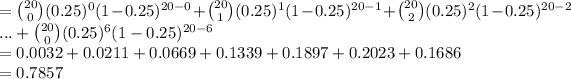
Thus, the probability that at most 6 will come to a complete stop is 0.7857.