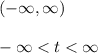Answer:
a.
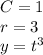
b.
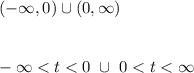
c.
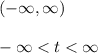
Explanation:
a. Solving as a separable equation.
Divide both sides by y:
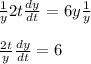
Divide both sides by 2t and multiply both sides by dt:
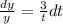
Integrate both sides:
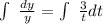
Evaluate the integrals:
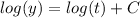
Where C is an arbitrary constant.
Solving for y:
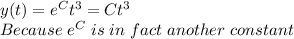
Evaluating the initial condition:

So:

b.
Let:
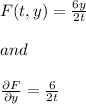
The domain of F(t,y) is:

The domain of
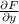 is:
is:

So, Existence and Uniqueness theorem tells us that for each
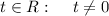 there exists a unique solution defined in an open interval around
there exists a unique solution defined in an open interval around

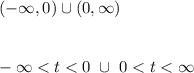
c. The domain of y(t) is:
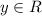
Hence, the actual interval of existence for the solution y(t) is: