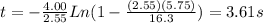Question

A rock with mass m = 4.00 kg falls from rest in a viscous medium. The rock is acted on by a net constant downward force of F = 16.3 N (a combination of gravity and the buoyant force exerted by the medium) and by a fluid resistance force f = kv, where v is the speed in m/s and k = 2.55 N×s/m .

1. Find the initial acceleration: a₀ = _______.
2. Find the acceleration when v = 2.10 m/s.
3. Find the speed when the acceleration equals 0.1*a₀.
4. Find the terminal speed
`V_t`.
5. Find the coordinate 2.00 s after the start of the motion.
6. Find the speed 2.00 s after the start of the motion.
7. Find the acceleration 2.00 s after the start of the motion.
8. Find the time required to reach a speed 0.9
`V_t`.

Answer 1

1)

The resistance force acting on the rock is:

`f=kv`

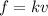
where

k = 2.55 Ns/m is a constant

v is the speed of the rock

At the beginning, the speed of the rock is zero, so the resistance force is also zero:

`f=0`

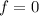
This means that the only force acting on the rock is the downward force:

F = 16.3 N

By applying Newton's second law,

`F=ma`

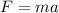
where

m = 4.00 kg is the mass of the rock

a is the acceleration

We find the initial acceleration:

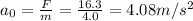`a_0 = (F)/(m)=(16.3)/(4.0)=4.08 m/s^2` (downward)

2)

When the speed is

v = 2.10 m/s

The fluid resistance force is:

`f=kv=(2.55)(2.10)=5.35 N`

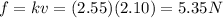
And this force is upward.

Therefore, the net force on the rock is:

`F-f`

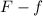
And so Newton's second law becomes

`F-f=ma`

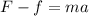
where

F = 16.3 N is the constant downward force

Solving for a, we find the new acceleration:

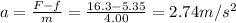`a=(F-f)/(m)=(16.3-5.35)/(4.00)=2.74 m/s^2` (downward)

3)

In this part, the acceleration of the rock is now equal to

`a=0.1a_0`

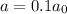
where

`a_0=4.08 m/s^2`

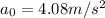
is the initial acceleration.

Therefore,

`a=0.1(4.08)=0.41 m/s^2`

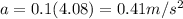
The acceleration is still downward, so we can write:

`F-f=ma`

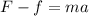
Rewriting the resistance,

`F-kv=ma`

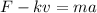
We can therefore solve the equation to find v, the speed of the rock:

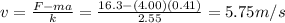`v=(F-ma)/(k)=(16.3-(4.00)(0.41))/(2.55)=5.75 m/s` (downward)

4)

The terminal speed occurs when the upward net force becomes equal to the downward net force: when this situation occurs, the net acceleration of the rock becomes zero, and the rock continues at constant velocity, which is called terminal speed.

As we said, the acceleration of the rock is now zero:

`a=0`

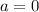
So Newton's second law becomes:

`F-f=0`

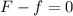
From which:

`F=f=kv`

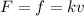
Therefore, the speed can be written as

`v=(F)/(k)`

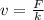
This is the terminal speed: therefore, it is equal to

`v_L = (16.3)/(2.55)=6.39 m/s`

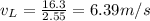
6)

Newton's second law at any point of motion can be written as

`a(t)=(F-kv)/(m)`

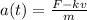
which gives an expression of the acceleration at time t.

We know that acceleration is the derivative of the velocity, so we can write the equation as:

`v'(t)=(F)/(m)-(k)/(m)v`

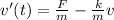
This is a differential equation; by integrating it, we find an expression for the speed at time t:

`v(t)=(F)/(k)(1-e^{-(k)/(m)t})`

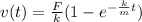
And by substituting

t = 2.00 s

We find the speed after 2.00 seconds:

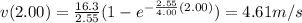`v(2.00)=(16.3)/(2.55)(1-e^{-(2.55)/(4.00)(2.00)})=4.61 m/s` (downward)

5)

To find the position of the rock at time t, we have to find an expression for x(t).

In part 6) we found an expression for the velocity at time t:

`v(t)=(F)/(k)(1-e^{-(k)/(m)t})`

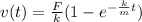
However, we know that the velocity is the derivative of the position x(t), so we can rewrite the equation as

`x'(t)=(F)/(k)(1-e^{-(k)/(m)t})`

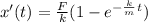
By integrating with respect to t, we can find an expression for x(t):

`x(t)=(F)/(k)(t+(m)/(k)e^{-(k)/(m)t})`

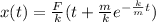
And now we can substitute

t = 2.00 s

To find the coordinate 2.00 s after the start of the motion:

`x(2.00)=(16.3)/(2.55)(2.00+(4.00)/(2.55)e^{-(2.55)/(4.00)(2.00)})=15.59 m`

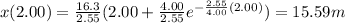
7)

Now we can find the acceleration of the rock 2.00 s after the start of the motion.

We know that the expression for the acceleration is (part 6):

`a(t)=(F-kv)/(m)`

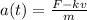
And we also know, again from part 6, that the velocity when t = 2.00 s is:

v = 4.61 m/s

Therefore, by substituting

F = 16.3 N

m = 4.00 kg

k = 2.55 Ns/m

We can now find the acceleration at t=2.00 s:

`a(2.00)=(16.3-(2.55)(4.61))/(4.00)=1.14 m/s^2`

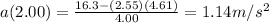
8)

Here we want to find the time required for the rock to reach a speed of

`v=0.9 v_L`

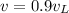
Where
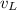`v_L` is the terminal speed.

From part 4), we know that the terminal speed is

`v_L = 6.39 m/s`

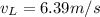
So in this part we want to find the time t at which the speed is

`v=0.9(6.39)=5.75 m/s`

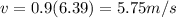
From part 6), we have an expression for the speed at time t:

`v(t)=(F)/(k)(1-e^{-(k)/(m)t})`

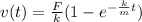
We can re-arrange it as:

`t=-(m)/(k)Ln(1-(kv)/(F))`

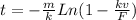
And by substituting v = 5.75 m/s and the other values, we find the time:

`t=-(4.00)/(2.55)Ln(1-((2.55)(5.75))/(16.3))=3.61 s`