Question

Solve the equation on the interval 0 less than or equals theta less than 2 pi .0≤θ<2π. secant StartFraction 5 theta Over 4 EndFraction equals 2sec 5θ 4=2 What is the solution set to secant StartFraction 5 theta Over 4 EndFraction equals 2sec 5θ 4=2 in the interval 0 less than or equals theta less than 2 pi0≤θ<2π​? Select the correct choice and fill in any answer boxes in your choice below. A. The solution set is StartSet nothing EndSet{ }. ​(Simplify your answer. Type an exact​ answer, using piπ as needed. Type your answer in radians. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as​ needed.) B. There is no solution. Click to select and enter your answer(s).

Answer 1

Answer: 4π/15, 4π/3 and 28π/15 (in radians)

Explanation:

[TeX]sec 5\theta/4 =2[/TeX]

Recall that [TeX]sec \theta = 1/cos \theta[/TeX]

[TeX] 1/cos (5\theta/4) =2[/TeX]

[TeX] cos (5\theta/4) =1/2[/TeX]

`Cos^(-1)`
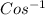
`(1)/(2)` = [TeX]5\theta/4[/TeX]

This implies that

[TeX]\mp60+360n=5\theta/4 [/TeX]

[TeX]\theta=4/5(\mp60+360n)= \mp48+288n [/TeX]

[TeX]When n=0, \theta=48 [/TeX]

[TeX]When n=1, \theta=240, 336 [/TeX]

Therefore the values of [TeX]\theta [/TeX] between 0 and 2π are 48, 240 and 336. (All in degrees)

48 degrees= 4π/15 rad

240 degrees =4π/3 rad

336 degrees = 28π/15 rad