Answer:
34.2 degrees.
Explanation:
Please find the attachment.
We have been given that Frank stands 450 feet from the base of the Statue of Liberty. If the Statue of Liberty is 306 feet tall. We are asked to find the angle of depression from the top of the statue’s torch to Frank.
Let x represent angle of depression.
We can see that angle of depression, Statue of liberty and Frank form a right triangle with respect to ground.
We know that tangent relates opposite side of right triangle with its adjacent side.
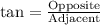
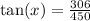
Now, we will inverse tangent to solve for x as:
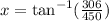
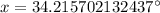
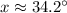
Therefore, the angle of depression would be approximately 34.2 degrees.