Question

A candle shop sells scented candles for $16 each and unscented candles for $10 each. The shop sells 28 candles today and makes $400.

Write a system of linear equations that represents the situation.
Please also include how many scented candles were sold and how many unscented were sold.
Thanks!!!

Answer 1

The system of linear equations that represents the situation is:

a + b = 28

16a + 10b = 400

20 scented candles and 8 unscented candles were sold

Solution:

Let "a" be the number of scented candles sold

Let "b" be the number of unscented candles sold

From given,

Cost of 1 scented candles = $ 16

Cost of 1 unscented candles = $ 10

The shop sells 28 candles today

Therefore,

a + b = 28

b = 28 - a ------- eqn 1

The shop sells 28 candles today and makes $400

Therefore,

number of scented candles sold x Cost of 1 scented candle + number of unscented candles sold x Cost of 1 unscented candles = 400

`a * 16 + b * 10 = 400`

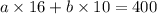
16a + 10b = 400 ------ eqn 2

Substitute eqn 1 in eqn 2

16a + 10(28 - a) = 400

16a + 280 - 10a = 400

6a = 400 - 280

6a = 120

a = 20

Substitute a = 20 in eqn 1

b = 28 - 20

b = 8

Thus 20 scented candles and 8 unscented candles were sold