Question

A bottling company uses a filling machine to fill plastic bottles with cola. The bottles are supposed to contain 300 milliliters (ml). In fact, the contents vary according to a Normal distribution with mean μ = 298 ml and standard deviation σ = 3 ml. What is the probability that the mean contents of six randomly selected bottles is less than 295 ml? a. 0.0478 b. 0.9928 c. 0.1587 d. 0.00002 e. 0.0072

Answer 1

e. 0.0072

Explanation:

We are given that a bottling company uses a filling machine to fill plastic bottles with cola. And the contents vary according to a Normal distribution with Mean, μ = 298 ml and Standard deviation, σ = 3 ml .

Let Z =
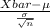`(Xbar - \mu)/((\sigma)/(√(n) ) )` ~ N(0,1) where, Xbar = mean contents of six randomly

selected bottles

n = sample size i.e. 6

So, Probability that the mean contents of six randomly selected bottles is less than 295 ml is given by, P(Xbar < 295)

P(Xbar < 295) = P(
`(Xbar - \mu)/((\sigma)/(√(n) ) )` <
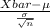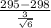`(295 - 298)/((3)/(√(6) ) )` ) = P(Z < -2.45) = P(Z > 2.45)

Now, using z% score table we find that P(Z > 2.45) = 0.00715 ≈ 0.0072 .

Therefore, option e is correct .