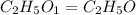Question

A 14.60g sample of an unknown compound, composed only of carbon, hydrogen, and oxygen, produced 28.6g of CO2 and 14.6g of H2O in a combustion analysis. What is the mass percent composition of oxygen of the unknown compound?

Answer 1

Answer: The empirical formula for the given compound is
`C_(2)H_(5)O`

Step-by-step explanation:

The chemical equation for the combustion of compound having carbon, hydrogen and oxygen follows:

`C_xH_yO_z+O_2\rightarrow CO_2+H_2O`

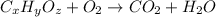
where, 'x', 'y' and 'z' are the subscripts of carbon, hydrogen and oxygen respectively.

We are given:

Mass of
`CO_2=28.6g`

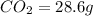
Mass of
`H_2O=14.6g`

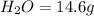
We know that:

Molar mass of carbon dioxide = 44 g/mol

Molar mass of water = 18 g/mol

For calculating the mass of carbon:

In 44 g of carbon dioxide, 12 g of carbon is contained.

So, in 28.6 g of carbon dioxide,
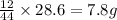`(12)/(44)* 28.6=7.8g` of carbon will be contained.

For calculating the mass of hydrogen:

In 18 g of water, 2 g of hydrogen is contained.

So, in 14.6 g of water,
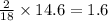`(2)/(18)* 14.6=1.6` of hydrogen will be contained.

For calculating the mass of oxygen:

Mass of oxygen in the compound = (14.60) - (7.8 + 1.6) = 5.2 g

To formulate the empirical formula, we need to follow some steps:

Step 1: Converting the given masses into moles.

Moles of Carbon =
`\frac{\text{Given mass of Carbon}}{\text{Molar mass of Carbon}}=(7.8g)/(12g/mole)=0.65moles`

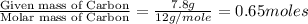
Moles of Hydrogen =
`\frac{\text{Given mass of Hydrogen}}{\text{Molar mass of Hydrogen}}=(1.6g)/(1g/mole)=1.6moles`

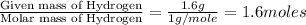
Moles of Oxygen =
`\frac{\text{Given mass of oxygen}}{\text{Molar mass of oxygen}}=(5.2g)/(16g/mole)=0.32moles`

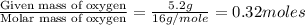
Step 2: Calculating the mole ratio of the given elements.

For the mole ratio, we divide each value of the moles by the smallest number of moles calculated which is 0.32 moles.

For Carbon =
`(0.65)/(0.32)=2.03\approx 2`

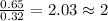
For Hydrogen =
`(1.6)/(0.32)=5`

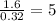
For Oxygen =
`(0.32)/(0.32)=1`

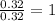
Step 3: Taking the mole ratio as their subscripts.

The ratio of C : H : O = 2 : 5 : 1

Hence, the empirical formula for the given compound is
`C_(2)H_(5)O_(1)=C_(2)H_(5)O`

Answer 2

`\large \boxed{35.4 \, \%}`

Step-by-step explanation:

Let's call the unknown compound X.

1. Calculate the mass of oxygen in 14.60 g of X.

(a) Mass of C

`\text{Mass of C} = \text{28.6 g CO}_(2)* \frac{\text{12.01 mg C}}{\text{44.01 mg }\text{CO}_(2)}= \text{7.805 g C}`

(b) Mass of H

`\text{Mass of H} = \text{14.6 g }\text{H$_(2)$O}* \frac{\text{2.016 g H}}{\text{18.02 g H$_(2)$O}} = \text{1.633 g H}`

(c) Mass of O

Mass of O = 14.60 - 7.805 - 1.633 = 5.162 g

2. Calculate the mass percent of oxygen