Question

A Pitot-static tube is used to measure the velocity of helium in a pipe. The temperature and pressure are 55oF and 28 psia. A water manometer connected to the Pitot-static tube indicates a reading of 2.3 in. (a) Determine the helium velocity. (b) Is it reasonable to consider the flow as incompressible

Answer 1

a) V=203 ft/s

b) Since the Mach number is 0.063 < 0.3, we can conclude that the flow

is incompressible!

Step-by-step explanation:

solution:

Start by deriving the expression for the fluid velocity, from the Bernoulli equation:

`p_0=p_(static) +(1)/(2) p_(fluid)V^2\\V=\sqrt{2(p_0-p_(static))/p_(fluid)}`

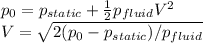
Next, we need to express the pressure difference between the stagnation pressure
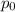`p_(0)` and the static pressure. This can be done using the relation between the pressures and the specific weights:

`p_(0)-p_(static)=(r_{manometer-r_(fluid)) } h`

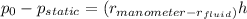
Since
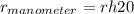`r_(manometer) =rh20` and it is much greater than
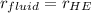`r_(fluid) =r_(HE)` we can obtain from the previous equation:

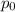`p_(0)`-p_static=
`r_(manometer)`h

V=√2*
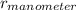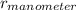`r_(manometer)`h/r_fluid

Using the ideal gas formula we can obtain the neccesarry density of Helium:

r_fluid=p/R.T

=5.80*10^-4 sl/ft^3

Using the value for water specific weight from the table B.1, we return to the expression for fluid velocity:

V=√2*
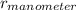`r_(manometer)`h/r_fluid

V=203 ft/s

Next, we need to obtain the Mach number for the fluid flow velocity, so that we can find out if the flow is in compressible or not. The Mach number formula is:

M=V/c

=V/√kRT

Substituting the known values for the real gas constant R, the given temperature T and the adiabatic index k, we obtain:

M=V/c

=0.063

Since the Mach number is 0.063 < 0.3, we can conclude that the flow is incompressible!