Question

Prove that cos⁻¹ (12/13) + sin⁻¹ (3/5) = sin⁻¹ (56/65)

Answer 1

`\text{L.H.S}\\\\=\cos^(-1) (12)/(13) + \sin^(-1) \frac 35\\\\=\sin^(-1) \frac 5{13} + \sin^(-1) \frac 35\\\\`

`=\sin^(-1)\left[\frac 5{13}√(1- \left(\frac 35 \right)^2) + \frac 35\sqrt{1-\left(\frac 5{13} \right)^2} \right]\\\\=\sin^(-1) \left(\frac 5{13} \sqrt{1-\frac 9{25} }+\frac 35 \sqrt{1-(25)/(169)} \right)\\\\=\sin^(-1) \left(\frac 5{13} \sqrt{(16)/(25)}+\frac 35 \sqrt{(144)/(169)} \right)\\\\=\sin^(-1) \left((5)/(13) \cdot \frac 45 + \frac 35 \cdot (12)/(13) \right)\\`

`=\sin^(-1) \left(\frac 4{13} +(36)/(65)\right)\\\\=\sin^(-1) \left((20)/(65) + (36)/(65) \right)\\\\=\sin^(-1) \left((20+36)/(65) \right)\\\\=\sin^(-1) \left((56)/(65) \right)\\\\=\text{R.H.S}`

Answer 2

See below ↓

Explanation:

We need to prove :

⇒ cos⁻¹
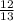`(12)/(13)` + sin⁻¹
`(3)/(5)` = tan⁻¹
`(56)/(65)`

Let's simplify the LHS.

• cos⁻¹
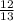  `(12)/(13)` + sin⁻¹
  `(3)/(5)`

Convert the inverse cos and sin functions into inverse tan functions

• tan⁻¹
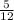  `(5)/(12)` + tan⁻¹
  `(3)/(4)`
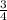
• [∴This can be found taking a right triangle and labeling the sides, and then using Pythagorean Theorem, we can find the missing side and take the ratio of tan]

Identity

• tan⁻¹ x + tan⁻¹ y = tan⁻¹
  `(x+y)/(1-xy)`

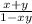
Using this identity, we can simplify our earlier equation!

⇒ tan⁻¹ [(5/12 + 3/4)/(1 - (5/12 x 3/4))]

⇒ tan⁻¹ [(20 + 36) / (48 - 15)

⇒ tan⁻¹ (56/65)

⇒ RHS

⇒ Proved ∴√