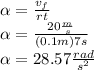Question

A rod of length 20 cm has two beads attached to its ends. The rod with beads starts rotating from rest. If the beads are to have a tangential speed of 20 m/s in 7 s, what is the angular acceleration of the rod to achieve this?

Answer 1

`\alpha=28.57(rad)/(s^2)`

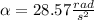
Step-by-step explanation:

We use the following rotational kinematic equation to calculate the angular acceleration of the rod:

`\omega_f=\omega_0+\alpha t`

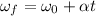
Here
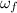`\omega_f` is the final angular speed,
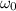`\omega_0\\` is the initial angular speed and
`\alpha` is the angular acceleration. The rod starts rotating from rest (
`\omega_0=0`):

`\alpha=(\omega_f)/(t)(1)`

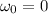Recall that the angular speed is defined in function of the tangential speed (v) and the radius (r) of the circular motion:

`w_f=(v_f)/(r)(2)`

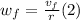
In this case the radius is given by
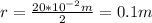`r=(20*10^(-2)m)/(2)=0.1m`. Replacing (2) in (1):

`\alpha=(v_f)/(rt)\\\alpha=(20(m)/(s))/((0.1m)7s)\\\alpha=28.57(rad)/(s^2)`