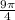Question

A wheel of radius 1 rolls along a straight line, say the r-axis. A point P is located halfway between the center of the wheel and the rim; assume P starts at the point (0, 1/2). As the wheel rolls, P traces a curve; find parametric equations for the curve. Erercises 10.5. 2. Consider the curve of exercise 6 in section 10.4. Find the area under one arch of the curve. Final answer is 9?/4

Answer 1

Part a: The parametric equations of the curve are as indicated
`x=(1)/(2)(\theta-sin \theta)\\y=(1)/(2)+(1)/(2)(1-cos \theta)`

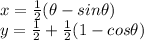
Part b: The area under the curve is
`(9 \pi)/(4)`

Explanation:

Part a

As the wheel rolls the path traced by the point is a cycloid which is as given as

`x=(r)/(2)(\theta-sin \theta)\\y=(1)/(2)+(r)/(2)(1-cos \theta)`

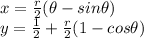
As the radius is 1 the equation is

`x=(1)/(2)(\theta-sin \theta)\\y=(1)/(2)+(1)/(2)(1-cos \theta)`

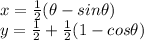
The parametric equations of the curve are as indicated above.

Part b

The area under the curve is given as

`\int_(0)^(2 \pi) ydx`

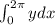
Here

y is given as

`y=(1)/(2)+(1)/(2)(1-cos \theta)`

and x is given as

`x=(1)/(2)(\theta-sin \theta)`

Finding its differential as

`{dx}=[(1)/(2)-cos \theta]}d\theta`

Substituting in the equation and solving the equation

`\int_(0)^(2 \pi) ydx\\\int_(0)^(2 \pi) [(1)/(2)+(1)/(2)(1-cos \theta)][(1)/(2)-cos \theta]}d\theta]\\\int_(0)^(2 \pi) [((cos(\theta)-2)(2cos(\theta)-1))/(4)d\theta]\\=(9 \pi)/(4)`

So the area under the curve is
`(9 \pi)/(4)`