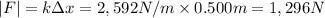Answer:
- 1. Part A: 648N
- 2. Part B: 324J
- 3. Part C: 1,296N
Step-by-step explanation:
1. Part A:
The magnitude of the force is calculated using the Hook's law:
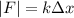
You know
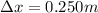 but you do not have
but you do not have
 .
.
You can calculate it using the equation for the work-energy for a spring.
The work done to compress the springs a distance
 is:
is:
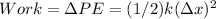
Where
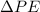 is the change in the elastic potential energy of the "spring".
is the change in the elastic potential energy of the "spring".
Here you have two springs, but you can work as if they were one spring.
You know the work (81.0J) and the length the "spring" was compressed (0.250m). Thus, just substitute and solve for k:

In reallity, the constant of each spring is half of that, but it is not relevant for the calculations and you are safe by assuming that it is just one spring with that constant.
Now calculate the magnitude of the force:
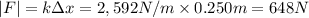
2. Part B. How much additional work must you do to move the platform a distance 0.250 m farther?
The additional work will be the extra elastic potential energy that the springs earn.
You already know the elastic potential energy when Δx = 0.250m; now you must calculate the elastic potential energy when Δx = 0.250m + 0.250m = 0.500m.
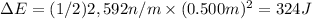
Therefore, you must do 324J of additional work to move the plattarform a distance 0.250 m farther.
3. Part C
What maximum force must you apply to move the platform to the position in Part B?
The maximum force is when the springs are compressed the maximum and that is 0.500m
Therefore, use Hook's law again, but now the compression length is Δx = 0.500m