Question

The 2000 census "long form" asked the total 1999 income of the householder, the person in whose name the dwelling unit was owned or rented. This census form was sent to a random sample of 17% of the nation's households. Suppose that the households that returned the long form are an SRS of the population of all households in each district. In Middletown, a city of 40,000 persons, 2621 householders reported their income. The mean of the responses was x = $33,453, and the standard deviation was s = $8721. The sample standard deviation for so large a sample will be very close to the population standard deviations. Use these facts to give an approximate 99% confidence interval for the 1999 mean income of Middletown householders who reported income.

Answer 1

The 99% confidence interval for the 1999 mean incomes of Middletown householders is ($33,013.5, $33,892.5).

Explanation:

Of the 40,000 persons, 2621 householders reported their income.

The sample size of the study is, n = 2621.

As the sample size is large, i.e. n > 30 use z-distribution to compute the confidence interval.

The confidence interval for mean is:

`CI=\bar x\pm z_(\alpha /2)(\sigma)/(√(n))`

The mean of this sample is,
`\bar x=\$33,453`

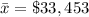
The standard deviation is,
`s\approx\sigma=\$8,721`

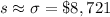
The critical value of z for 99% confidence level is:

`z_(\alpha /2)=z_(0.01/2)=z_(0.005)=2.58`

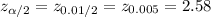
The 99% confidence interval for the 1999 mean incomes of Middletown householders is:

`CI=\bar x\pm z_(\alpha /2)(\sigma)/(√(n))\\=33453\pm2.58*(8721)/(√(2621))\\=33453\pm439.50\\=(33013.5, 33892.5)`

Thus, the 99% confidence interval for the 1999 mean incomes of Middletown householders is ($33,013.5, $33,892.5).