Question

The quantity demanded per month, x, of a certain make of personal computer (PC) is related to the average unit price, p (in dollars), of PCs by the equationx = f(p) =1009810,000 − p2It is estimated that t mo from now, the average price of a PC will be given byp(t) =4001 +18t+ 200 (0 ≤ t ≤ 60)dollars. Find the rate at which the quantity demanded per month of the PCs will be changing 16 mo from now. (Round your answer to one decimal place.)

Answer 1

The value of dx/dt is
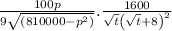`(100p)/(9√((810000-p^2))).(1600)/(√(t)\left(√(t)+8\right)^2)\\` while the rate of change of quantity demanded per month after 16 months is 18.7.

Explanation:

From the given data the equation of quantity demanded for average price is given as is given as

`x=f(p)=(100)/(9)√(810000-p^2)`

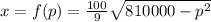
The equation of average price p for a given value of t is given as

`p(t)=(400)/(1+(1)/(8)√(t))+200`

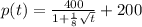
Now in order to determine the rate at which the quantity demanded will be changing is given as
`(dx)/(dt)`

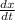
This is found by using the chain rule as

`(dx)/(dt)=(dx)/(dp).(dp)/(dt)`

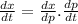
Now

`(dx)/(dp)=(d((100)/(9)√(810000-p^2)))/(dp)\\(dx)/(dp)=(100)/(9)(d)/(dp)[(810000-p^2)^(1/2)]\\(dx)/(dp)=(100)/(9)(1)/(2)[(810000-p^2)^(-1/2)](d)/(dp)[(810000-p^2)]\\(dx)/(dp)=(50)/(9)[(810000-p^2)^(-1/2)](-2p)\\(dx)/(dp)=(100p)/(9√((810000-p^2)))`

Now

`\\(dp)/(dt)=(d((400)/(1+(1)/(8)√(t))+200))/(dt)\\(dp)/(dt)=(d)/(dt)\left((400)/(1+(1)/(8)√(t))+200\right)\\(dp)/(dt)=(d)/(dt)\left((400)/(1+(1)/(8)√(t))\right)+0\\(dp)/(dt)=400(d)/(dt)\left((1)/(1+(1)/(8)√(t))\right)\\(dp)/(dt)=400(d)/(du)\left(\left(1+(1)/(8)√(t)\right)^(-1)\right)(d)/(dt)\left(1+(1)/(8)√(t)\right)\\(dp)/(dt)=-(1600)/(√(t)\left(√(t)+8\right)^2)`

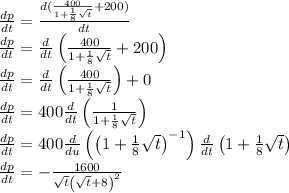
So now the value of dx/dt is given as

`(dx)/(dt)=(dx)/(dp).(dp)/(dt)\\(dx)/(dt)=(100p)/(9√((810000-p^2))).(1600)/(√(t)\left(√(t)+8\right)^2)\\`

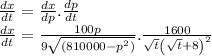
So the value of dx/dt is
`(100p)/(9√((810000-p^2))).(1600)/(√(t)\left(√(t)+8\right)^2)\\`

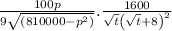
Now for the time =16 months price is given as

`p(t)=(400)/(1+(1)/(8)√(t))+200\\p(16)=(400)/(1+(1)/(8)√(16))+200\\p(16)=466.67`

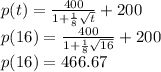
Now the value of x is given as

`(dx)/(dt)=(100p)/(9√((810000-p^2))).(1600)/(√(t)\left(√(t)+8\right)^2)\\\\(dx)/(dt)=(100*466.67)/(9√((810000-466.67^2))).(1600)/(√(16)\left(√(16)+8\right)^2)\\(dx)/(dt)=18.72`

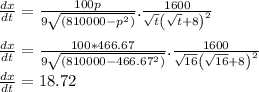
So the rate of change of quantity demanded per month after 16 months is 18.72