Question

A phone manufacturer wants to compete in the touch screen phone market. Management understands that the leading product has a less than desirable battery life. They aim to compete with a new touch screen phone that is guaranteed to have a battery life more than two hours longer than the leading product. A recent sample of 102 units of the leading product provides a mean battery life of 5 hours and 40 minutes with a standard deviation of 93 minutes. A similar analysis of 56 units of the new product results in a mean battery life of 8 hours and 53 minutes and a standard deviation of 84 minutes. It is not reasonable to assume that the population variances of the two products are equal. All times are converted into minutes. Let new products and leading products represent population 1 and population 2, respectively.

Calculate the value of the test statistic. (Round all intermediate calculations to at least 4 decimal places and final answer to 2 decimal places.)

Answer 1

Explanation:

Hello!

To compete in the touch screen phone market a manufacturer aims to release a new touch screen with a battery life said to last more than two hours longer than the leading product which is the desired feature in phones.

To test this claim two samples were taken:

Sample 1

X: battery lifespan of a unit of the new product (min)

n= 93 units of the new product

mean battery life X[bar]= 8:53hs= 533min

S= 84 min

Sample 2

X: battery lifespan of a unit of the leading product (min)

n= 102 units of the leading product

mean battery life X[bar]= 5:40 hs = 340min

S= 93 min

The population variances of both variances are unknown and distinct.

To test if the average battery life of the new product is greater than the average battery life of the leading product by 2 hs (or 120 min) the parameters of interest will be the two population means and we will test their difference, the hypotheses are:

H₀: μ₁ - μ₂ ≤ 120

H₁: μ₁ - μ₂ > 120

Considering that there is not enough information about the distribution of both variables, but both samples are big enough, we can apply the central limit theorem and approximate the distribution of both sample means to normal, this way we can use the standard normal:

`Z= \frac{(X[bar]_1-X[bar]_2)-(Mu_1-Mu_2)}{\sqrt{(S_1^2)/(n_1) +(S_2^2)/(n_2) } }`

Z≈N(0;1)

`Z= \frac{(533-340)-120}{\sqrt{(84^2)/(56) +(93^2)/(102) } }= 5.028`

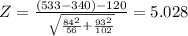
I hope this helps!