The sum we want is
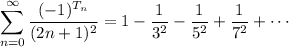
where
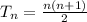 is the n-th triangular number, with a repeating sign pattern (+, -, -, +). We can rewrite this sum as
is the n-th triangular number, with a repeating sign pattern (+, -, -, +). We can rewrite this sum as
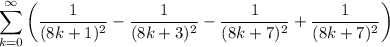
For convenience, I'll use the abbreviations
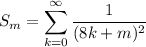
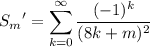
for m ∈ {1, 2, 3, …, 7}, as well as the well-known series
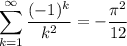
We want to find
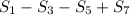 .
.
Consider the periodic function
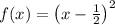 on the interval [0, 1], which has the Fourier expansion
on the interval [0, 1], which has the Fourier expansion
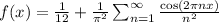
That is, since f(x) is even,
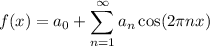
where
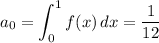
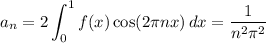
(See attached for a plot of f(x) along with its Fourier expansion up to order n = 10.)
Expand the Fourier series to get sums resembling the
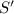 -s :
-s :
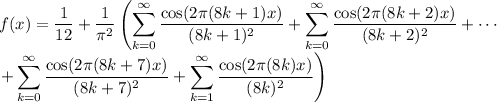
which reduces to the identity
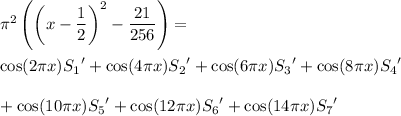
Evaluating both sides at x for x ∈ {1/8, 3/8, 5/8, 7/8} and solving the system of equations yields the dependent solution
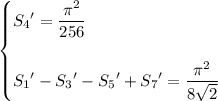
It turns out that
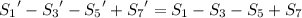
so we're done, and the sum's value is
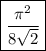 .
.