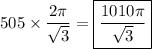Recall the geometric sum,
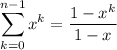
It follows that
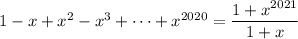
So, we can rewrite the integral as
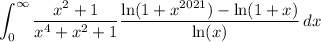
Split up the integral at x = 1, and consider the latter integral,
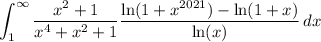
Substitute
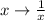 to get
to get
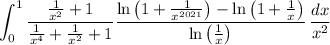
Rewrite the logarithms to expand the integral as
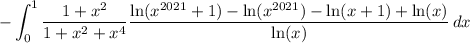
Grouping together terms in the numerator, we can write
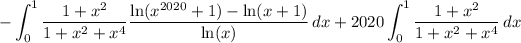
and the first term here will vanish with the other integral from the earlier split. So the original integral reduces to
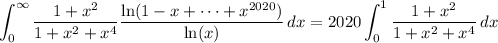
Substituting
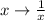 again shows this integral is the same over (0, 1) as it is over (1, ∞), and since the integrand is even, we ultimately have
again shows this integral is the same over (0, 1) as it is over (1, ∞), and since the integrand is even, we ultimately have
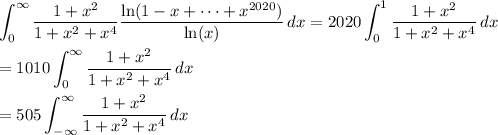
We can neatly handle the remaining integral with complex residues. Consider the contour integral
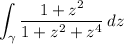
where γ is a semicircle with radius R centered at the origin, such that Im(z) ≥ 0, and the diameter corresponds to the interval [-R, R]. It's easy to show the integral over the semicircular arc vanishes as R → ∞. By the residue theorem,
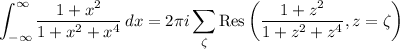
where
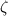 denotes the roots of
denotes the roots of
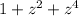 that lie in the interior of γ; these are
that lie in the interior of γ; these are
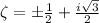 . Compute the residues there, and we find
. Compute the residues there, and we find
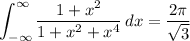
and so the original integral's value is