Question

A group of adult males has foot lengths with a mean of 26.88 cm and a standard deviation of 1.13 cm. Use the range rule of thumb to

limits separating values that are significantly low or significantly high. Is the adult male foot length of 24.3 cm significantly low or signific
Explain.
Significantly low values are
cm or lower.
- din
a t round​

Answer 1

Using the range rule of thumb, a foot length of 24.3 cm is significantly low compared to an average of 26.88 cm with a standard deviation of 1.13 cm since it is below the low-end cutoff of 24.62 cm.

Step-by-step explanation:

The question is related to the concept of normal distribution and uses the range rule of thumb to identify what could be considered unusually low or high measurements of adult male foot length. The range rule of thumb generally considers values below the mean minus two times the standard deviation as significantly low, and values above the mean plus two times the standard deviation as significantly high.

To evaluate whether an adult male foot length of 24.3 cm is significantly low, we apply this rule to the given data with a mean (average) foot length of 26.88 cm and a standard deviation of 1.13 cm. So, we calculate the low-end cutoff as 26.88 - 2(1.13) = 24.62 cm. A foot length of 24.3 cm is below this cutoff, therefore it can be considered significantly low within this context.

Answer 2

The adult male foot length of 24.3 cm is significantly low.

Step-by-step explanation:

We have been given that a group of adult males has foot lengths with a mean of 26.88 cm and a standard deviation of 1.13 cm. We are asked to find the range rule of thumb to determine whether he adult male foot length of 24.3 cm significantly low or significantly high.

The range rule of thumb states that usual values in a normal standard deviation lies within 2 standard deviation from mean that is
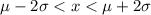`\mu-2\sigma<x<\mu+2\sigma`, where
`\mu=\text{ Mean and }\sigma=\text{Standard deviation}`.

Let us find the range of possible values.

`28.88-2(1.13)<x<28.88+2(1.13)`

`28.88-2.26<x<28.88+2.26`

`26.62<x<31.14`

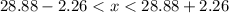
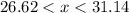
Since 24.3 is less than lower value of range (26.62), therefore, the adult male foot length of 24.3 cm is significantly low.