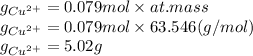Question

A current of 3.53 A is passed through a Cu ( NO 3 ) 2 solution for 1.20 h . How much copper is plated out of the solution?

Answer 1

10.035 g of Cu deposited.

Step-by-step explanation:

Equation of the reaction:

Cu(NO3)2 --> Cu2+ + 2NO3^-

Q = It

Where,

I = current

= 3.53 A

t = time

= 1.2 h * 3600 s/1 h

= 4320 s

Q = 4320 * 3.52

= 15249.6 C

1 mole of metal deposited contains 96500C.

Therefore,

Number of moles = 15249.6/96500

= 0.158 mol of Cu deposited.

Mass = number of moles * molar mass

= 0.158 * 63.5

= 10.035 g of Cu deposited.

Answer 2

The amount of Cu²⁺ plated out is 5.02 g.

Step-by-step explanation:

To solve the problem we must first consider the following equation

Cu²⁺ + 2e -------> Cu (s) ---------- (1)

This equation shows that two moles of electrons are used for the conversion of Cu²⁺. So let us first determine the number of moles of electrons, which can be calculated from the following formula

`n=(I* t)/(F)`

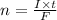
Here, I is the current in ampere, t is time in seconds and F is the Faraday's constant. Placing the data we get,

`n=(3.53* 1.2* 3600)/(9.648*10^(4))`

`n=0.158 mol`

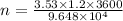
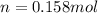
Equation 1 shows that 1 mole of Cu²⁺ consumes two moles of electrons. So, the moles of Cu²⁺ will be half of the moles of electrons.

`n_(Cu^(2+))=(0.158)/(2) mol\\n_(Cu^(2+))=0.079 mol`

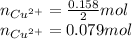
the mass of Cu²⁺ will be

`g_(Cu^(2+)) = 0.079 mol * at.mass\\g_(Cu^(2+)) = 0.079 mol * 63.546 (g/mol)\\g_(Cu^(2+)) = 5.02 g`