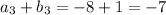Question

The first two terms of a sequence are a1=4 and a2=-2. Let a3 be the third term when the sequence is arithmetic and let b3 be the third term when the sequence is geometric.Find a3+b3

Answer 1

As

`a_3=-8` ;
`b_3=1`

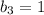
Therefore,

`a_3+b_3=-8+1=-7`

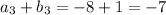
Explanation:

Considering the first two terms of a sequence

`a_1=4\:;\:a_2=-2`

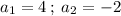
Finding
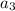`a_3` when the sequence is arithmetic

Let
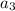`a_3` be the third term when the sequence is arithmetic.

The common difference = d = -2 - 4 = -6

The n-th term of Arithmetic sequence is:

`a_n=a_1+\left(n-1\right)d`

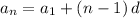
Putting n = 3 in the n-th term to find
`a_3` .

`a_n=a_1+\left(n-1\right)d`

`a_3=4+\left(3-1\right)\left(-6\right)`

`a_3=4-12`

`a_3=-8`

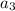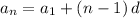
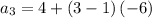
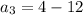
Finding
`b_3` when the sequence is geometric

Let
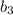`b_3` be the third term when the sequence is geometric.

The common ratio r is:

`r=-(2)/(4)=-(1)/(2)`

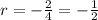
The n-th term of a geometric sequence with initial value b and common ratio r is given by

`b_(n)=b\,r^(n-1)`

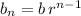
Putting n = 3 in the n-th term to find
`b_3` .

`b_3=4\cdot \left(-(1)/(2)\right)^(3-1)`

`b_3=4\cdot (1)/(2^2)` ∵
`\left(-(1)/(2)\right)^(3-1)=(1)/(2^2)`

`b_3=(1\cdot \:4)/(2^2)`

`b_3=(2^2)/(2^2)`

`b_3=1`

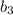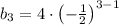
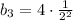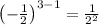
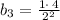
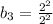
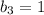
So,

`a_3=-8` ;
`b_3=1`

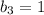
Therefore,

`a_3+b_3=-8+1=-7`