Question

Two 2.0-cm-diameter insulating spheres have a 6.60 cm space between them. One sphere is charged to + 76.0 nC , the other to - 30.0 nC . Part A What is the electric field strength at the midpoint between the two spheres? Express your answer with the appropriate units.

Answer 1

`5.2* 10^5N/C`

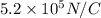
Step-by-step explanation:

Since the two charged bodies are symmetric, we can calculate the electric field taking both of them as point charges.

This can be easily seen if we use Gauss's law,
`\int{E} \, dA=(Q_(enclosed))/(\epsilon_o)`

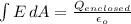
We take a larger sphere of radius, say r, as the Gaussian surface. Then the electric field due to the charged sphere at a distance r from it's center is given by,

`E=(1)/(4\pi r^2) (Q_(enclosed))/(\epsilon_o)`

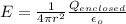
which is the same as that of a point charge.

In our problem the charges being of opposite signs, the electric field will add up. Therefore,

`E_(total)=(1)/(4\pi\epsilon_o)(q_1+q_2)/(r^2)= (9*10^9) ((76+30)*10^(-9))/(((1+3.3)*10^(-2))^2)N/C =5.2*10^5N/C`

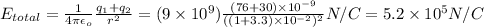
where,
`r` = distance between the center of one sphere to the midpoint (between the 2 spheres)