Answer:
4, −3, 1 over 5
Explanation:
x is a zero of
 if
if
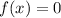
In this problem, we have that:
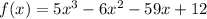
4, 3, 1 over 5
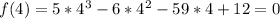
So 4 is a zero of the function
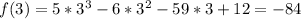
So 3 is not a zero of the function, and this option is incorrect
4, 3, − 1 over 5
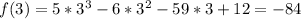
So 3 is not a zero of the function, and this option is incorrect
4, −3, 1 over 5
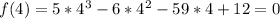
So 4 is a zero of the function
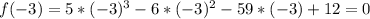
So -3 is a zero of the function
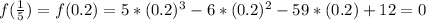
So 1 over 5 is a zero of the function
This is the correct answer.
4, −3, −1 over 5
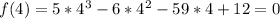
So 4 is a zero of the function
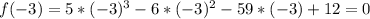
So -3 is a zero of the function
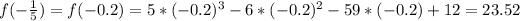
-1 over 5 is not a zero of the function