Question

The computers of nine engineers at a certain company are to be replaced. Four of the engineers have selected laptops and the other 5 have selected desktops. Suppose that four computers are randomly selected. (a) How many different ways are there to select four of the nine computers to be set up?

(b) What is the probability that exactly three of the selected computers are desktops?

(c) What is the probability that at least three desktops are selected?

Answer 1

a) There are 126 different ways are there to select four of the nine computers to be set up.

b) 31.75% probability that exactly three of the selected computers are desktops.

c) 35.71% probability that at least three desktops are selected.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

In this problem, there are no replacements. Which means that after one of the 9 computers is selected, there will be 8 computers.

Also, the order that the computers are selected is not important. For example, desktop A and desktop B is the same outcome as desktop B and desktop A.

These are the two reasons why the combinations formula is important to solve this problem.

Combinations formula:

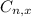`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

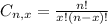
(a) How many different ways are there to select four of the nine computers to be set up?

Four computers are selected from a set of 9.

So

`T = C_(9,4) = (9!)/(4!(9-4)!) = 126`

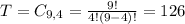
There are 126 different ways are there to select four of the nine computers to be set up.

(b) What is the probability that exactly three of the selected computers are desktops?

Desired outcomes:

3 desktops, from a set of 5

One laptop, from a set of 4.

So

`D = C_(5,3)*C_(4,1) = 40`

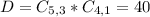
Total outcomes:

From a), 126

Probability:

`P = (40)/(126) = 0.3175`

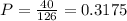
31.75% probability that exactly three of the selected computers are desktops.

(c) What is the probability that at least three desktops are selected?

Three or four

Three:

`P = (40)/(126)`

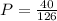
Four:

Desired outcomes:

4 desktops, from a set of 5

Zero laptop, from a set of 4.

`D = C_(5,4)*C_(4,0) = 5`

`P = (5)/(126)`

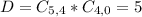
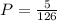
Total(three or four) probability:

`P = (40)/(126) + (5)/(126) = (45)/(126) = 0.3571`

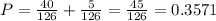
35.71% probability that at least three desktops are selected.