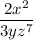Question

Need help ASAP

Simplify using only positive exponents

1.) 3^2•3^4

2.) (2x^2)^-4

3.) 2x^4y^-4z^-3
————————-
3x^2y^-3z^4

Answer 1

Part (1) : The solution is
`729`

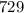
Part (2): The solution is
`$(1)/(16 x^(8))$`

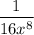
Part (3): The solution is
`$(2 x^(2))/(3 y z^(7))$`

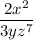
Step-by-step explanation:

Part (1): The expression is
`3^(2) \cdot3^(4)`

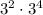
Applying the exponent rule,
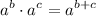`$a^(b) \cdot a^(c)=a^(b+c)$`, we get,

`$3^(2) \cdot 3^(4)=3^(2+4)$`

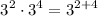
Adding the exponent, we get,

`3^(2) \cdot3^(4)=3^6=729`

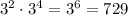
Thus, the simplified value of the expression is
`729`

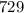
Part (2): The expression is
`$\left(2 x^(2)\right)^(-4)$`

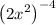
Applying the exponent rule,
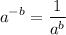`$a^(-b)=(1)/(a^(b))$`, we have,

`$\left(2 x^(2)\right)^(-4)=(1)/(\left(2 x^(2)\right)^(4))$`

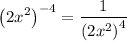
Simplifying the expression, we have,

`(1)/(2^4x^8)`

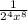
Thus, we have,

`$(1)/(16 x^(8))$`

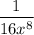
Thus, the value of the expression is
`$(1)/(16 x^(8))$`

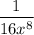
Part (3): The expression is
`$(2 x^(4) y^(-4) z^(-3))/(3 x^(2) y^(-3) z^(4))$`

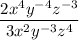
Applying the exponent rule,
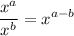`$(x^(a))/(x^(b))=x^(a-b)$`, we have,

`(2x^(4-2)y^(-4+3)z^(-3-4))/(3)`

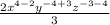
Adding the powers, we get,

`(2x^(2)y^(-1)z^(-7))/(3)`

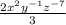
Applying the exponent rule,
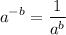`$a^(-b)=(1)/(a^(b))$`, we have,

`$(2 x^(2))/(3 y z^(7))$`

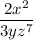
Thus, the value of the expression is
`$(2 x^(2))/(3 y z^(7))$`