Question

-A: Find the force that must be exerted on the rod to maintain a constant current of 0.156 A in the resistor? (In mN)

-B: What is the rate of the energy dissipation in the resistor? (In W)

-C: What is the mechanical power delivered to the rod? (In W)

Answer 1

A) Force: 0.0528 N

B) Power dissipated: 0.307 W

C) Power delivered: 0.307 W

Step-by-step explanation:

A)

The force experienced by a current-carrying wire in a magnetic field is given by

`F=ILB`

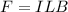
where

I is the current in the wire

L is the length of the wire

B is the strength of the magnetic field

In this problem, we have:

L = 0.451 m

B = 0.751 T

I = 0.156 A

Therefore, the force is

`F=(0.156)(0.451)(0.751)=0.0528 N`

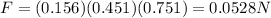
B)

The rate of energy dissipation in the resistor is the power dissipated in the resistor, and it is given by

`P=I^2R`

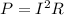
where

I is the current in the resistor

R is the resistance

For the wire in this problem,

I = 0.156 A

`R=12.6\Omega`

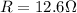
Therefore, the power dissipated is

`P=(0.156)^2(12.6)=0.307 W`

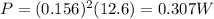
C)

The mechanical power delivered to the rod is given by

`P=VI`

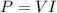
where

V is the potential difference across the rod

I is the current in the rod

The potential difference across the rod must be equal to the potential difference across the resistance, which can be found by using Ohm's law:

`V=RI=(12.6 \Omega)(0.156 A)=1.97 V`

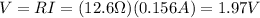
Therefore, the power delivered to the rod is

`P=(1.97 V)(0.156 A)=0.307 W`

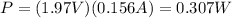
This power is equal to the power dissipated on the resistor: this is due to the law of conservation of energy, in fact the total energy must remain constant, so here the electric energy is transformed into mechanical energy of motion of the rod.