Question

What is the area of this trapezoid? 86 in² 112 in² 148 in² 184 in² Trapezoid A B C D with parallel sides D C and A B. Point F and E are on side D C. Point F is connected to point A by a dotted segment. Point E is connected to point B by a dotted segment. A B E F is a rectangle. D F is 3 inches. E C is 6 inches. E B is 8 inches. A B is 14 inches.

Answer 1

Option C:
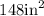`$148 \mathrm{in}^(2)$` is the area of the trapezoid.

Step-by-step explanation:

The image of the trapezoid having these descriptions is attached below:

Now, we shall determine the area of the trapezoid using the formula,

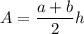`$A=(a+b)/(2) h$` where a and b are the base of the trapezoid and h is the height of the trapezoid.

Thus, we shall find the value of a and b from the diagram given below.

`a= AB=14in`

`b=DC\\b=DF+FE+EC\\b=3+14+6\\b=23in`

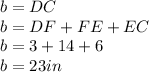
It is given that the height of the trapezoid
`h=8in`

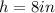
Thus, substituting the values of a,b and h in the formula
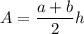`$A=(a+b)/(2) h$`, we get,

`A=(14+23)/(2)(8)\\ A=(37)/(2) (8)\\A=148in^2`

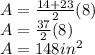
Thus, the area of the trapezoid is
`$148 \mathrm{in}^(2)$`

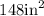
Hence, Option C is the correct answer.