Question

What is x given ABC~DBE.
Show your work

Answer 1

x = 37.5 (or)
`(75)/(2)`

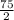
Solution:

Given
`\triangle A B C \sim \triangle D B E`

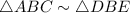
AC = 50, DE = 30, EC = 25, BE = x, BC = 25 + x

To find the value of x:

Property of similar triangles:

If two triangles are similar then the corresponding angles are congruent and the corresponding sides are in proportion.

`$(BE)/(BC) =(DE)/(AC)`

`$(x)/(25+x) =(30)/(50)`

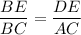
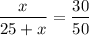
Do cross multiplication, we get

`50x=30(25+x)`

`50x=750+30x`

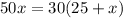
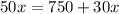
Subtract 30x from both sides of the equation.

`20x=750`

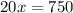
Divide by 20 on both sides of the equation, we get

x = 37.5 (or)
`(75)/(2)`

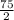
Hence the value of x is 37.5 or
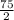`(75)/(2)`.