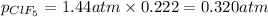Question

A tank at is filled with of boron trifluoride gas and of chlorine pentafluoride gas. You can assume both gases behave as ideal gases under these conditions. Calculate the mole fraction and partial pressure of each gas, and the total pressure in the tank. Be sure your answers have the correct number of significant digits. a. boron trifluoride mole fraction:b. partial pressure:c. chlorine pentafluoride mole fraction:d. partial pressure:d. Total pressure in tank:

Answer 1

The question is incomplete, here is the complete question:

A 5.00 L tank at 4.19°C is filled with 16.7 g of boron trifluoride gas and 9.15 g of chlorine pentafluoride gas. You can assume both gases behave as ideal gases under these conditions. Calculate the mole fraction and partial pressure of each gas, and the total pressure in the tank. Be sure your answers have the correct number of significant digits.

a. mole fraction of boron trifluoride:

b. partial pressure of boron trifluoride:

c. mole fraction of chlorine pentafluoride:

d. partial pressure of chlorine pentafluoride:

e. Total pressure in tank:

Answer:

For a: Mole fraction of boron trifluoride is 0.778

For b: Partial pressure of boron trifluoride is 1.12 atm

For c: Mole fraction of chlorine pentafluoride is 0.222

For d: Partial pressure of chlorine pentafluoride is 0.320 atm

For e: Total pressure in tank is 1.44 atm

Step-by-step explanation:

To calculate the number of moles, we use the equation:

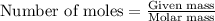`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}` .....(1)

• For boron trifluoride:

Given mass of boron trifluoride = 16.7 g

Molar mass of boron trifluoride = 67.8 g/mol

Putting values in equation 1, we get:

`\text{Moles of boron trifluoride}=(16.7g)/(67.8g/mol)=0.246mol`

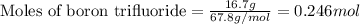
• For chlorine pentafluoride:

Given mass of chlorine pentafluoride = 9.15 g

Molar mass of chlorine pentafluoride = 130.5 g/mol

Putting values in equation 1, we get:

`\text{Moles of chlorine pentafluoride }=(9.15g)/(130.5g/mol)=0.070mol`

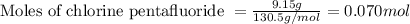
To calculate the pressure of the tank, we use the equation given by ideal gas which follows:

`PV=nRT`

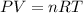
where,

P = pressure of the tank = ?

V = Volume of the tank = 5.00 L

T = Temperature of the gas =
`4.19^oC=[4.19+273]K=277.19K`

R = Gas constant =
`0.0821\text{ L.atm }mol^(-1)K^(-1)`

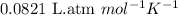
n = Total number of moles of the tank = [0.246 + 0.070] = 0.316 moles

Putting values in above equation, we get:

`P* 5.0L=0.316mol* 0.0821\text{ L.atm }mol^(-1)K^(-1)* 277.19K\\\\P=(0.316* 0.0821* 277.19)/(5.0)=1.44atm`

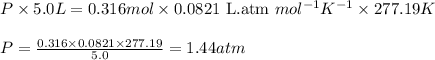
Mole fraction of a substance is given by:

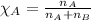`\chi_A=(n_A)/(n_A+n_B)` .......(2)

To calculate the partial pressure, we use the equation given by Raoult's law, which is:

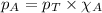`p_(A)=p_T* \chi_(A)` .....(3)

• For boron trifluoride:

Moles of boron trifluoride = 0.246 moles

Total moles = 0.316 moles

Putting values in equation 2, we get:

`\chi_(BF_3)=(0.246)/(0.316)=0.778`

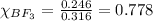
We are given:

`p_T=1.44atm\\\chi_(BF_3)=0.778`

Putting values in equation 3, we get:

`p_(BF_3)=1.44atm* 0.778=1.12atm`

• For chlorine pentafluoride:

Moles of chlorine pentafluoride = 0.070 moles

Total moles = 0.316 moles

Putting values in equation 2, we get:

`\chi_(ClF_5)=(0.070)/(0.316)=0.222`

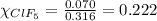
We are given:

`p_T=1.44atm\\\chi_(ClF_5)=0.222`

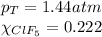
Putting values in equation 3, we get:

`p_(ClF_5)=1.44atm* 0.222=0.320atm`