Question

Suppose that 70% of the statisticians are shy, whereas 30% of the economist are shy. Suppose also that 80% of the people at a large gathering are economists and the remaining 20% are statisticians. If you randomly meet a person at the gathering and the person is shy, what is the probability that the person is a statistician?

Answer 1

The probability that a randomly selected person who is shy is a Statistician is 0.3684.

Explanation:

Let's denote the events as follows:

E = a person is an Economist

S = a person is a Statistician

X = a person is shy.

Given:

P (E) = 0.80

P (S) = 0.20

P (X|S) = 0.70

P (X|E) = 0.30

Compute the probability that a randomly selected person is shy is:

`P(X) = P(X|S)P(S)+P(X|E)P(E)\\=(0.70*0.20)+(0.30*0.80)\\=0.38`

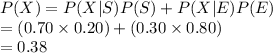
The probability that a person is shy is, P (X) = 0.38.

The conditional probability of an event A provided that another event B has already occurred is:

`P(A|B)=(P(B|A)P(A))/(P(B))`

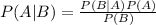
Compute the probability that a randomly selected person who is shy is a Statistician as follows:

`P(S|X)=(P(X|S)P(S))/(P(X))=(0.70*0.20)/(0.38)= 0.3684`

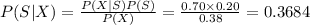
Thus, the probability that a randomly selected person who is shy is a Statistician is 0.3684.